viernes, 30 de septiembre de 2016
martes, 27 de septiembre de 2016
Mapa del sitio
martes, 20 de septiembre de 2016
Recorrido por la civilización india en la historia de la matemática
Resumen:
El presente video presenta un recorrido histórico por los
principales aportes a la matemática por parte de la civilización india. Allí,
Shirley Gómez aborda desde sus inicios hasta la época actual, los principales
escritos y autores que dieron un lugar en la historia la matemática india.
Por lo tanto se habla de sus inicios, pasando por sus
primeros registros representados en los Sulvasutras en la construcción de
templos, pasando por los Siddhantas donde se descubre la función Seno, luego
Aryabhata con el sistema posicional de base 10, de ahí hasta Brahmagupta con su
aporte al usar los números negativos y el cero, Bhaskara con la definición de
indeterminado para finalizar con Ramanujar y sus aportes en el siglo XX.
Abstract:
This video
presents a historical overview of the main contributions to mathematics by the
Indian civilization. There, Shirley Gomez approached from its beginnings to the
present day, the main writings and authors given a place in the history of
Indian mathematics.
So talking
about his beginnings, through his first records represented in the Sulvasutras
in building temples, through the Siddhantas where the sine function is
discovered, then Aryabhata with positional base 10 system, hence to Brahmagupta
with its contribution to use negative numbers and zero, Bhaskara with the
definition of indeterminate, ending with Ramanujar and their contributions in
the twentieth century.
Referencia bibliográfica:
Corrales, A. F. (2016, septiembre 19).
Recorrido por la civilización india en la historia de la matemática [Archivo de
video]. Recuperado de https://youtu.be/j3bmBVYSKCM
Etiquetas:
ENTREVISTA AL EXPERTO
La civilización China
A
pesar de que los desarrollos matemáticos de la antigua Grecia comenzaban a
tambalearse durante los últimos siglos antes de Cristo, el floreciente imperio
comercial de China fue líder de las matemáticas a alturas cada vez mayores.
El
antiguo sistema de numeración chino simple pero eficiente, se remonta a por lo
menos al segundo milenio antes de Cristo. Utiliza pequeñas varas de bambú
dispuestas para representar los números 1 a 9, que eran entonces lugares en
columnas que representan las unidades, decenas, cientos, miles, etc. Por lo
tanto, era un sistema de valores decimales, muy similar a la que usamos hoy en
día. De hecho, fue el primer sistema de numeración, aprobado por los chinos más
de mil años antes de que fuera adoptado en Occidente, logrando hacer incluso
cálculos muy complejos de manera rápida y fácil.
Para
los números escritos, sin embargo, emplearon un sistema ineficiente porque utilizaban
un símbolo diferente para decenas, cientos, miles, etc. en gran parte porque no
existía el concepto del Cero, lo que tuvo el efecto de limitar la utilidad de
la escritura de los números para los chinos.
El
uso del ábaco es a menudo considerado como una idea china, pero algún tipo de
ábaco fue utilizado en Mesopotamia, Egipto y Grecia, probablemente mucho antes
que en China (el primer ábaco chino, o “suanpan”, en fechas aproximadamente del
segundo siglo antes de Cristo).
Había
una fascinación generalizada por números y patrones matemáticos en la antigua
China, y diferentes números tienen significado cósmico. En particular, los
cuadrados mágicos, que son cuadrados de números en los que cada fila, columna y
diagonal suman lo mismo, estos se dice que tienen un gran significado
espiritual y religioso.
Un
caso muy representativo de esto es el de Lo Shu, un cuadrado mágico que suma
15. Según la leyenda, un cierto día por el tercer milenio a. C. se produjo el
desbordamiento de un río; la gente, temerosa, intentó hacer una ofrenda al dios
del río Lo (uno de los desbordados) para calmar su ira. Sin embargo, cada vez
que lo hacían, aparecía una tortuga que rondaba la ofrenda sin aceptarla, hasta
que un chico se dio cuenta de las peculiares marcas del caparazón de la
tortuga, de este modo pudieron incluir en su ofrenda la cantidad pedida (15),
quedando el dios satisfecho y volviendo las aguas a su cauce.
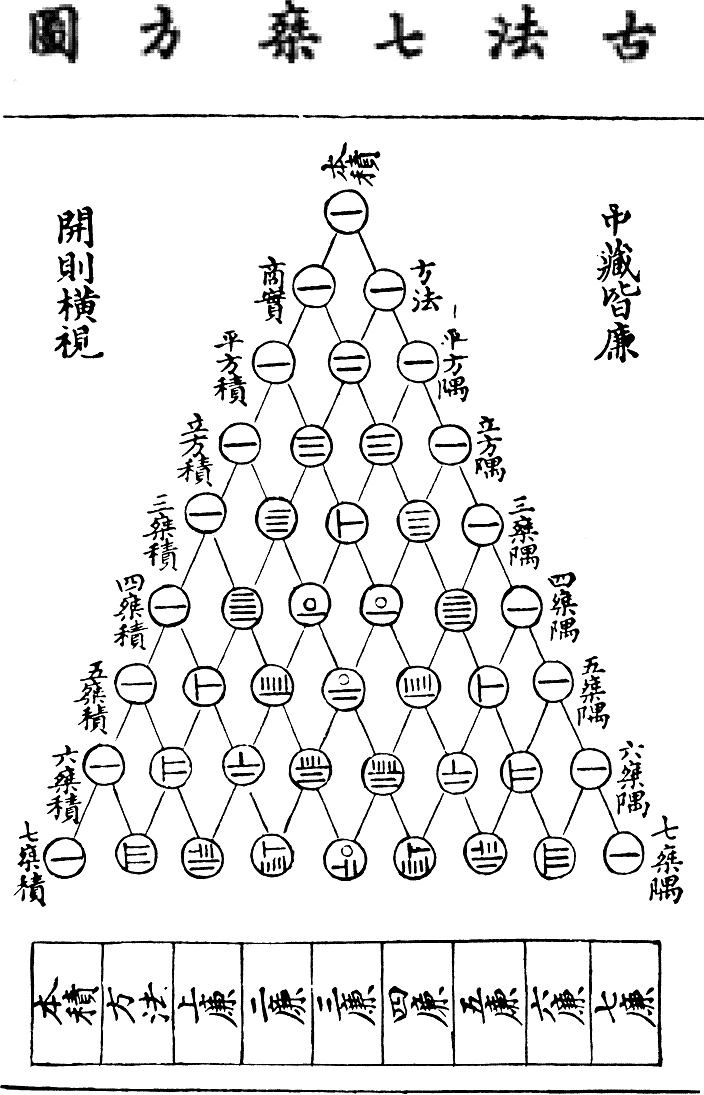
Estos registros datan de alrededor del año 650
a. C. y continuó su desarrollo hasta el siglo XIII en el que Yang Hui trabajó
en los cuadrados mágicos, los círculos mágicos y el teorema del binomio; es
reconocido por su presentación del Triángulo Yang Hui. Este triángulo,
descubierto por su predecesor Xian Yang Jia, era el mismo que el triángulo de
Pascal.
El
objetivo principal de las matemáticas chinas fue desarrollado en respuesta a la
creciente necesidad del imperio para hacer que los administradores fueran matemáticamente
competentes. Un libro de texto llamado “Jiuzhang suanshu” o “Nueve capítulos
del arte matemático” (escrito alrededor del 200 a. C. por una variedad de autores) se convirtió en
una herramienta importante en la educación de este tipo de servicio civil, que incluyó
cientos de problemas en áreas prácticas, tales como el comercio, la fiscalidad,
la ingeniería y el pago de salarios.
Fue
particularmente importante como guía para resolver ecuaciones, utilizando un
método basado en la matriz sofisticada. Aquella que no apareció en Occidente
hasta que Carl Friedrich Gauss la redescubrió a principios del siglo XIX y que
ahora se conoce como la eliminación de Gauss. También desarrolla de unas primeras
formas de cálculo integral y diferencial.
Los
chinos pasaron a resolver ecuaciones mucho más complejas y comenzaron a
perseguir los problemas matemáticos más abstractos (aunque generalmente
expresada en términos prácticos y no artificiales), incluyendo lo que se conoce
como el teorema chino del residuo. Este utiliza el residuo después de dividir un número desconocido
por una sucesión de números más pequeños, tales como 3, 5 y 7, con el fin de
calcular el valor más pequeño del número desconocido.
Una
técnica para resolver este tipo de problemas, inicialmente planteados por Sun
Tzu en el siglo III d. C. y considerado una de las joyas de la matemática,
estaba siendo utilizado para medir los movimientos planetarios por los
astrónomos chinos en el siglo VI. Aún hoy tiene usos prácticos en disciplinas
como la criptografía.
En
el siglo XIII, la edad de oro de las matemáticas chinas, había más de 30
escuelas de matemáticos prestigiosos dispersos en toda China. Tal vez el
matemático chino más brillante de esta época fue Qin Jiushao, un administrador
imperial bastante violento, corrupto y guerrero, que exploró soluciones a ecuaciones
cuadráticas e incluso cúbicas utilizando un método de aproximaciones repetidas
muy similar a la que más tarde desarrollado en Occidente por Newton en el siglo
XVII. Qin incluso extendió su técnica para resolver (aproximadamente)
ecuaciones con números elevados hasta la potencia de diez, algo extraordinariamente
complejo para su tiempo.
Referencias bibliográficas:
Penalva, Á. y Martínez, J. (2016). Breve
Historia de las Matemáticas: La Edad Contemporánea (I): Universidad politécnica
de Cartagena. Cartagena, España. Recuperado de
http://www.upct.es/seeu/concursos/Breve_Historia_Matematicas_contemporanea.pdf
De J. O. (2015). Historia de la
Matemáticas primera parte: REDSOCIAL56. Recuperado de:
https://redsocial56.com/2015/02/15/historia-de-las-matematicas/
Brahmagupta
La
biografía que viene a continuación fue tomada de EcuRed y nos adentra en la
vida de Brahmagupta:
Fue
un matemático y astrónomo indio. Fue el jefe del observatorio astronómico en
Ujjain, y durante su mandato allí escribió cuatro textos sobre las matemáticas
y la astronomía: Cadamekela en el 624, Brahmasphutasiddhanta en 628,
Khandakhadyaka en 665, y Durkeamynarda en 672.
Su
padre fue Jisnugupta. Nació en el año 598, posiblemente en Ujjain, donde vivió.
En esta ciudad de la zona central de la India se encontraba el más famoso y
antiguo observatorio de astronomía del que Brahmagupta era el director. Está
considerado el más grande de los matemáticos de esta época. Murió en el año
670.
Es
posible que Brahmagupta haya sido el idealizador del concepto del
"cero" ya que en su obra Brahmasphutasiddhanta del año 628 aparece
por primera vez esta idea. La obra trataba también sobre aritmética y números
negativos en términos muy parecidos a los de la moderna matemática.
Su
actividad tuvo lugar en Ujjain, en el noroeste de la India, zona que, durante
siglos antes y después de él, constituyó el núcleo central de la ciencia
indostana. Brahmagupta resumió sus conocimientos astronómicos en un libro
escrito en el año 628, y en este rechazaba la rotación de la Tierra, idea esta
que algunos astrónomos indostanos defendían.
El
rasgo más notable del libro es la aplicación de métodos algebraicos a los
problemas astronómicos. Ciertamente, los matemáticos indostanos rindieron un
gran servicio al mundo, ya que, en una fecha indeterminada situada dentro de
los dos siglos siguientes, un matemático anónimo ideó el concepto y el símbolo
«cero». Esto prestaba a la notación posicional importancia práctica y,
consiguientemente, se adoptó un sistema numérico basado en dicha notación. Este
sistema se extendió a los árabes, como en el caso de Al-Khwarizmi, y a partir
de ellos fue introducido en Europa (los «números arábigos» en uso hoy en día)
por hombres como Fibonacci.
Referencia bibliográfica:
Brahmagupta, (s. f). En EcuRed.
Recuperado el 20 de septiembre de 2016 de https://www.ecured.cu/Brahmagupta
____________________
Brahmagupta
Early Life
and Work
Brahmagupta was an Indian mathematician, born
in 598 AD in Bhinmal, a state of Rajhastan, India. He spent most of his life in
Bhinmal which was under the rule of King Vyaghramukha. He was the head of the
astronomical observatory at Ujjain which was the center of mathematics in India
witnessing the work of many extraordinary mathematicians.
Brahmagupta wrote many textbooks for
mathematics and astronomy while he was in Ujjain. These include ‘Durkeamynarda’
(672), ‘Khandakhadyaka’ (665), ‘Brahmasphutasiddhanta’ (628) and ‘Cadamakela’
(624). The ‘Brahmasphutasiddhanta’ meaning the ‘Corrected Treatise of Brahma’
is one of his well-known works. It contains a lot of criticism on the work of
his rival mathematicians. Brahmagupta had many discrepancies with his fellow
mathematicians and most of the chapters of this book talked about the loopholes
in their theories.
Contributions
to Mathematics
One of the most significant input of
Brahmagupta to mathematics was the introduction of ‘zero’ to the number system
which stood for ‘nothing’. His work the ‘Brahmasphutasiddhanta’ contained many
mathematical findings written in verse form. It had many rules of arithmetic
which is part of the mathematical solutions now. These are ‘A positive number
multiplied by a positive number is positive.’, ‘A positive number multiplied by
a negative number is negative’, ‘A negative number multiplied by a positive
number is negative’ and ‘A negative number multiplied by a negative number is
positive’. The book also consisted of many geometrical theories like the
‘Pythagorean Theorem’ for a right angle triangle. Brahmagupta was the one to
give the area of a triangle and the important rules of trigonometry such as
values of the sin function. He introduced the formula for cyclic
quadrilaterals. He also gave the value of ‘Pi’ as square root ten to be
accurate and 3 as the practical value. Additionally he introduced the concept
of negative numbers.
Contribution
to Science and Astronomy
Brahmagupta argued that the Earth and the
universe are round and not flat. He was the first to use mathematics to predict
the positions of the planets, the timings of the lunar and solar eclipses.
Though all this seems like obvious and simple solutions it was a major
improvement in science at that time. He also calculated the length of the solar
year which was 365 days, 5 minutes and 19 seconds which is quite accurate based
on today’s calculation of 365 days, 5 hours and 19 seconds. He also talked
about ‘gravity’ in one of his statements saying: ‘Bodies fall towards the earth
as it is in the nature of the earth to attract bodies, just as it is in the
nature of water to flow’.
Death
This great mathematician died between 660 and
670. He was one of the greatest mathematicians in Indian history and his
contributions to mathematics and science have made major differences to various
mathematical problems by establishing the basic rules which now allow us to
find their solutions. He was honored by the title given to him by a fellow
scientist ‘Ganita Chakra Chudamani’ which is translated as ‘The gem of the
circle of mathematicians’.
Referencia bibliográfica:
Brahmagupta,
(s. f). En Famous Mathematicians. Recuperado el 20 de septiembre
de 2016 de http://www.famous-mathematicians.com/brahmagupta/
La civilización India
Resumen:
La civilización India
A continuación se presenta un recorrido histórico por los
principales aportes a la matemática por parte de la civilización india. Allí,
se abordan desde sus inicios hasta la época actual los principales
escritos y autores que dieron un lugar en la historia la matemática india.
Por lo tanto se habla de sus inicios, pasando por sus
primeros registros representados en los Sulvasutras en la construcción de
templos, pasando por los Siddhantas donde se descubre la función Seno, luego
Aryabhata con el sistema posicional de base 10, de ahí hasta Brahmagupta con su
aporte al usar los números negativos y el cero.
Abstract:
Next, we present a historical overview of the main contributions to mathematics by the Indian civilization. There, the main writings and authors given a place in the history of Indian mathematics is approached from its beginnings to the present day.
So talking about his beginnings, through his early writings represented in the Sulvasutras in building temples, through the Siddhantas where the sine function is discovered, then Aryabhata with positional base 10 system, hence to Brahmagupta with its contribution to use negative numbers and zero.
La civilización India
Hay una falta de continuidad de la
tradición en la matemática hindú. Por lo que las contribuciones importantes han
aparecido como episodios separados en periodos de tiempo largos, sin
continuidad.
Es
muy probable los primeros registros se hayan dado antes de la mítica fundación
de Roma en el 753 a. C. donde usaron sus conocimientos geométricos primitivos
para la medición de templos y la medición y construcción de altares, adoptando
la forma de un cuerpo de conocimiento conocido como Sulvasutras, que viene de
unir los términos Sulva, que significa cuerdas para efectuar mediciones, y
Sutra que se refiere a un libro de reglas o aforismos relativos a cierto ritual
o ciencia.
El
más conocido de los Sulvasutras es el Apastamba, donde se encuentran reglas
para la construcción de ángulos rectos por medio de cuerdas cuyas medidas
constituyen ternas pitagóricas. Luego, todas estas ternas se pueden derivar
fácilmente de la vieja regla babilónica para construirlas, por lo cual es
probable que tuvieran una influencia mesopotámica. Es así como Apastamba sabía
la forma general del teorema de Pitágoras, que bien pudo haber sido tomada de
Mesopotamia.
Estos
libros han sigo datados por los historiadores dentro de un intervalo de casi
mil años, desde el siglo VIII a. C. hasta el siglo II de nuestra era. Luego de
esto sigue la época de los Siddhantas o sistemas astronómicos. Se trata de
cinco libros de los cuales solo uno, el Surya Siddhanta o “Sistema del Sol” se
conserva completo. Son teorías griegas mezcladas con el viejo Folclore hindú
escrito hacia el año 400.
Si
bien esta influencia es palpable, los conocimientos trigonométricos adquiridos
de Alejandría tomaron una forma significativa en manos de los hindúes. Esto
porque:
Mientras
la trigonometría de Ptolomeo se basaba en la relación funcional entre las
cuerdas y sus correspondientes arcos o ángulos centrales, que ellas subtienden,
los escritores de los Siddhantas transformaron esto para convertirlo en un
estudio de la correspondencia entre la mitad de la cuerda y la mitad del arco o
del ángulo central subtendido por la cuerda total.
Esto
no es más que el nacimiento de la función trigonométrica moderna Seno. Por lo
tanto, se puede afirmar que esta ha sido la contribución principal de los
hindúes a la a la historia de la matemática.
Ya
para el siglo sexto, Aryabhata escribió el Araybhatiya, que es una recopilación
de desarrollos anteriores. Básicamente hizo una compilación de varios autores
de los cuales no se tenían registros escritos, más que pequeños fragmentos.
Escrita en verso con el objeto de suplementar las reglas de cálculo utilizadas
en astronomía.
En
la segunda mitad de este libro se encuentra un elemento nuevo que dejaría
huella en la historia: el sistema de numeración posicional decimal. Así,
Aryabhata afirmaba que “de un lugar a otro, cada uno es diez veces el que le
precede”. Ellos reconocieron que por el principio posicional las cifras que
representan los nueve primeros números sirven también como cifra para los
correspondientes múltiplos de diez y por consiguiente a cualquier potencia de
diez.
Este
sistema quedó completo cuando Brahmagupta introduce el cero para representar la
nada además adicional a la forma de operar con él y de las operaciones con
números negativos. Por lo tanto, lo que se llama el sistema hindú consiste en
tres principios básicos: 1. Una base decimal, 2. Una notación posicional y 3.
Una forma cifrada para cada uno de los diez numerales básicos.
Ninguno
de estos principios fue creado por los hindúes, pero lo que sí hicieron fue
reunirlos para construir el sistema de numeración moderno.
Representantes civilización India
Referencia bibliográfica:
Boyer Carl, B. (1999). Historia de la Matemática. Alianza Editorial. Madrid, España.
La civilización Árabe
La civilización Árabe
Su
tradición inicial se dio con los estudios de Tabit Ibn Qurra sobre los números
amigos. No se sabe cómo continuó, salvo que en el siglo XI, Ibn al – Haytham
resolvió problemas de congruencia y que al – Farisi logró nuevos resultados
respecto a la descomposición de un número en factores primos. Los números
amigos que fueron estudiados por Al Madshritti (muerto en 1007), Abu Mansur
Tahir al-Baghdadi (980-1037), Pierre de Fermat(1601-1665), René Descartes
(1596-1650), a quien se atribuye a veces la fórmula de Tabit, C. Rudolphus y
otros. La fórmula de Tabit fue generalizada por Euler.
Si
un número es amigo de sí mismo (es igual a la suma de sus divisores propios),
recibe el nombre de número perfecto.
Una
segunda tradición fue sugerida por el estudio de la Aritmética de Diofanto
traducida parcialmente por Qusta Ibn Luqa, la cual suscitó investigaciones
sobre la resolución de sistemas de ecuaciones indeterminadas con soluciones
enteras o racionales y sobre las tríadas pitagóricas. La tercera dirección
concierne al estudio de las series y de series finitas que aparecen en ciertos
problemas de álgebra, de probable origen preislámico.
Se
reencuentran estos problemas en el capítulo sobre el cálculo de superficies y
volúmenes (por el método de exhaución), cuyo origen se remonta a Arquímedes, y
en el de los números figurados, cuyo estudio se reactivó gracias a la traducción
de la Introducción a la Aritmética de Nicómaco.
Sobre
la primera tradición, sólo se ha podido constatar en los textos de al – Andalus
y el Magreb el tema de los números amigos. AI – Mutaman, matemático de
Zaragoza, insertó en su tratado una nueva traducción del opúsculo de Tabit Ibn
Qurra, y encontramos cálculos de parejas de números amigos en las obras de al –
Hassar (siglo XII) y Ibn Munçim.
Puesto
que ninguno de sus libros se tradujo al latín o al hebreo, no se sabe a través
de qué canales circularon esos temas por Europa.
La
segunda tradición se halla presente en el Occidente musulmán en forma de
problemas resueltos en obras de álgebra, pero no se menciona a Diofanto ni a
los matemáticos árabes inspirados por él.
Una
tercera tradición se manifiesta en el capítulo de la ciencia del cálculo que
trata problemas relativos a la suma y sabemos que su contenido circuló por
Europa, bien fuera en escritos latinos y hebreos o en traducciones de textos
árabes.
En
Geometría se genera una primera tradición a partir de problemas de
constructividad de puntos y figuras planas. Tras enfrentarse a menudo con
construcciones irresolubles, algunos matemáticos islámicos extendieron la
noción de existencia geométrica o algebraica mediante la utilización
sistemática de las secciones cónicas. Se realizaron estudios sobre las
propiedades de tales curvas y sobre los mejores medios para engendrarlas. Ello
permitió resolver, de nuevas y múltiples maneras, los problemas clásicos de la
tradición griega: trisección del ángulo, duplicación del cubo, inscripción de
polígonos regulares en el círculo. Más tarde, diferentes contribuciones
favorecieron la elaboración de la teoría geométrica de las ecuaciones cúbicas.
Una
segunda tradición geométrica se dedicó a los problemas de medida (superficies,
volúmenes, momento de inercia), lo que permitió volver a obtener resultados
perdidos de Arquímedes (como la determinación del área de una sección de
parábola) y completar otros.
La
tercera tradición geométrica árabe, nacida de una lectura crítica de los
Elementos de Euclides, permitirá extender las operaciones aritméticas a los
irracionales positivos, elaborar nuevas reflexiones sobre los fundamentos de la
Geometría (en particular, sobre el postulado de las paralelas) y redefinir el
concepto de razón, lo que permitiría establecer la noción de número real
positivo.
Paralelamente
se desarrolló otro tipo de reflexión hasta el siglo XI, concerniente a los
problemas de construcción y razonamiento geométricos, que luego se extendió a
todos los instrumentos de demostración (análisis y síntesis, reducción al
absurdo, inducción). De hecho es una verdadera tradición, constituida a partir
de elementos ya presentes en el corpus filosófico y matemático griego. Sus
artífices son Tabit Ibn Qurraa en el siglo IX, Ibrahim Ibn Sinan y as-Siji en
el siglo X, Ibn al-Haytham en el XI, y probablemente otros cuyos escritos no
han llegado hasta nosotros y que futuras investigaciones podrían revelar.
Se
ha comenzado a determinar aspectos relativos a la circulación de esas diferentes
tradiciones geométricas orientales. Respecto a la primera, disponemos de dos
testimonios poco conocidos que permiten asegurar que llegó a al – Andalus y al
Magreb. El matemático magrebí Ibn Haydur menciona dos escritos orientales sobre
la inscripción del heptágono. Se trata de las epístolas de as-Sagani (siglo X)
y de Abu Muhammad. El mismo autor menciona un texto atribuido a un matemático
hindú que toma como valor aproximado del lado del heptágono inscrito la mitad
del lado del triángulo equilátero inscrito en el círculo.
El
segundo testimonio, mucho más importante, es el del filósofo zaragozano Ibn
Bajá, Avempace para los latinos, que da informaciones precisas sobre los
trabajos de su profesor Ibn Sayyid, de Valencia, y sobre sus propios trabajos concernientes
al estudio de las cónicas y su uso para generar nuevas curvas planas, que
habrían sido usadas para resolver dos generalizaciones de problemas clásicos:
el de la determinación de n medias proporcionales entre dos magnitudes dadas
(que generaliza el problema para dos medias, resuelto ya por los griegos) y el
de la multisección de un ángulo (que generaliza el de la trisección).
Hay
que señalar que en el siglo XII se consideraban ambas generalizaciones como no
resueltas todavía; al menos es lo que dice el gran matemático as –
Sama"wal. Este hecho por sí mismo nos permite afirmar no sólo que el
contenido del corpus geométrico clásico (cuyo conocimiento es indispensable
para dedicarse a problemas nuevos del mismo tipo) era conocido en ciertos foros
científicos hispanos, sino que sus matemáticos se hallaban bien informados
sobre los problemas en que trabajaban los matemáticos islámicos orientales y
participaron activamente en su resolución.
Para
la segunda tradición no se dispone más que de los libros de al – Mutaman, que
nunca se refiere explícitamente a sus fuentes, pero que debido a la diversidad
de temas tratados en sus obras y a las maneras en que lo hizo, se podría
afirmar que una gran parte de la tradición árabe relativa a Arquímedes llegó a
al – Andalus, incluso si las pruebas concretas de que se dispone, se refieren
solo al escrito de Ibrahim Ibn Sinan sobre el cálculo del área de una porción
de parábola.
En
lo que concierne a la tercera tradición, se sabe desde hace poco tiempo que la
contribución más importante de Ibn al – Haytham en este campo, su Libro sobre
el análisis y la síntesis, llegó a Zaragoza como muy tarde en la segunda mitad
del siglo XI. La copia sirvió para la redacción de algunos capítulos del libro
de al-Mutaman.
En
trigonometría, los primeros pasos dados en Oriente consistieron en extender y
mejorar las tablas hindúes de senos y cosenos, y luego introducir funciones
nuevas: tangente, cotangente, secante y cosecante. Más tarde se establecieron
las relaciones fundamentales entre estas seis funciones, siendo la más célebre
el teorema del seno, que servirá para el cálculo de los elementos del triángulo
esférico, y que sobre todo permitirá ahorrarse el uso del teorema de Menelao
(siglo I), instrumento menos efectivo para los calculistas.
La
importancia de estas nuevas herramientas llevaría a los astrónomos a dedicarles
capítulos autónomos. Es lo que hicieron Ibn Iraq, en Asia central y Abu l –
Wafa, en Bagdad. Esas contribuciones puramente matemáticas favorecieron el
proceso de autonomía de la trigonometría en relación a los problemas
astronómicos que permitieron su desarrollo. Esta autonomía está ya patente en
el libro de al – Biruni, Las claves de la Astronomía, y se completa en el
tratado de Nasir ad – Din at – Tusi, El libro de la figura secante.
No
hay elementos que permitan asegurar que estas dos últimas obras fueron
conocidas en Europa, pero eso no significa que los métodos y resultados que
contienen no hayan circulado mediante obras menos importantes o más
especializadas.
En
efecto, según el matemático magrebí del siglo XIV Ibn Haydur, el teorema del
seno era accesible en su época (y por tanto también en los siglos XII y XIII)
sea a través de una obra de Ibn Muadh (muerto después de 1050), un matemático
de Jaén, sea a través de otro especialista hispano, Jabir Ibn Aflah, sea a
través del apéndice añadido por el filósofo Avicena a su resumen del
Almagestode Ptolomeo. Ibn Haydur supone incluso que ningún escrito oriental de
trigonometría, distinto del de Avicena, llegó al Occidente musulmán. Si eso
fuera cierto habría ahí otro ejemplo de ruptura, aún inexplicada, en la
circulación de importantes resultados científicos.
Algunos representantes y sistemas de numeración:
Referencia bibliográfica:
Límaco, R. J. (2009). Historia de las
matemáticas: La civilización árabe. Monografías.com. Recuperado de
http://www.monografias.com/trabajos81/matematica-arabe/matematica-arabe3.shtml
Suscribirse a:
Comentarios (Atom)
:origin()/pre14/6f41/th/pre/f/2013/117/8/0/like_facebook_png_by_kimysviercz-d639w31.png)